Lab 3: Correspondence Analysis
Exercise 1 (Forest data)
Forest data includes the populations of eight species of trees growing on ten upland sites (A-J) in southern Wisconsin. We are going to perform correspondence analysis on this data in R and learn how to interpret the results.
We first load the following packages into the workspace.
library(FactoMineR)
library(factoextra)Read the forest data in R.
A <- c(9,8,5,3,2,0,0,0)
B <- c(8,9,4,4,2,0,0,0)
C <- c(3,8,9,0,4,0,0,0)
D <- c(5,7,9,6,5,0,0,0)
E <- c(6,0,7,9,6,2,0,0)
F <- c(0,0,7,8,0,7,0,5)
G <- c(5,0,4,7,5,6,7,4)
H <- c(0,0,6,6,0,6,4,8)
I <- c(0,0,0,4,2,7,6,8)
J <- c(0,0,2,3,5,6,5,9)
forest_dat <- data.frame(A,B,C,D,E,F,G,H,I,J)
rownames(forest_dat) <- c("BurOak", "BlackOak", "WhiteOak", "RedOak", "AmericanElm",
"Basswood", "Ironwood", "SugarMaple")We now call the library gplots and convert the raw data into a table.
library("gplots")
# convert the data as a table
dt <- as.table(as.matrix(forest_dat))
dt## A B C D E F G H I J
## BurOak 9 8 3 5 6 0 5 0 0 0
## BlackOak 8 9 8 7 0 0 0 0 0 0
## WhiteOak 5 4 9 9 7 7 4 6 0 2
## RedOak 3 4 0 6 9 8 7 6 4 3
## AmericanElm 2 2 4 5 6 0 5 0 2 5
## Basswood 0 0 0 0 2 7 6 6 7 6
## Ironwood 0 0 0 0 0 0 7 4 6 5
## SugarMaple 0 0 0 0 0 5 4 8 8 9The contingency table can be visualised using a balloonplot as below.
balloonplot(t(dt), main ="Forest data", xlab ="", ylab="",
label = FALSE, show.margins = TRUE)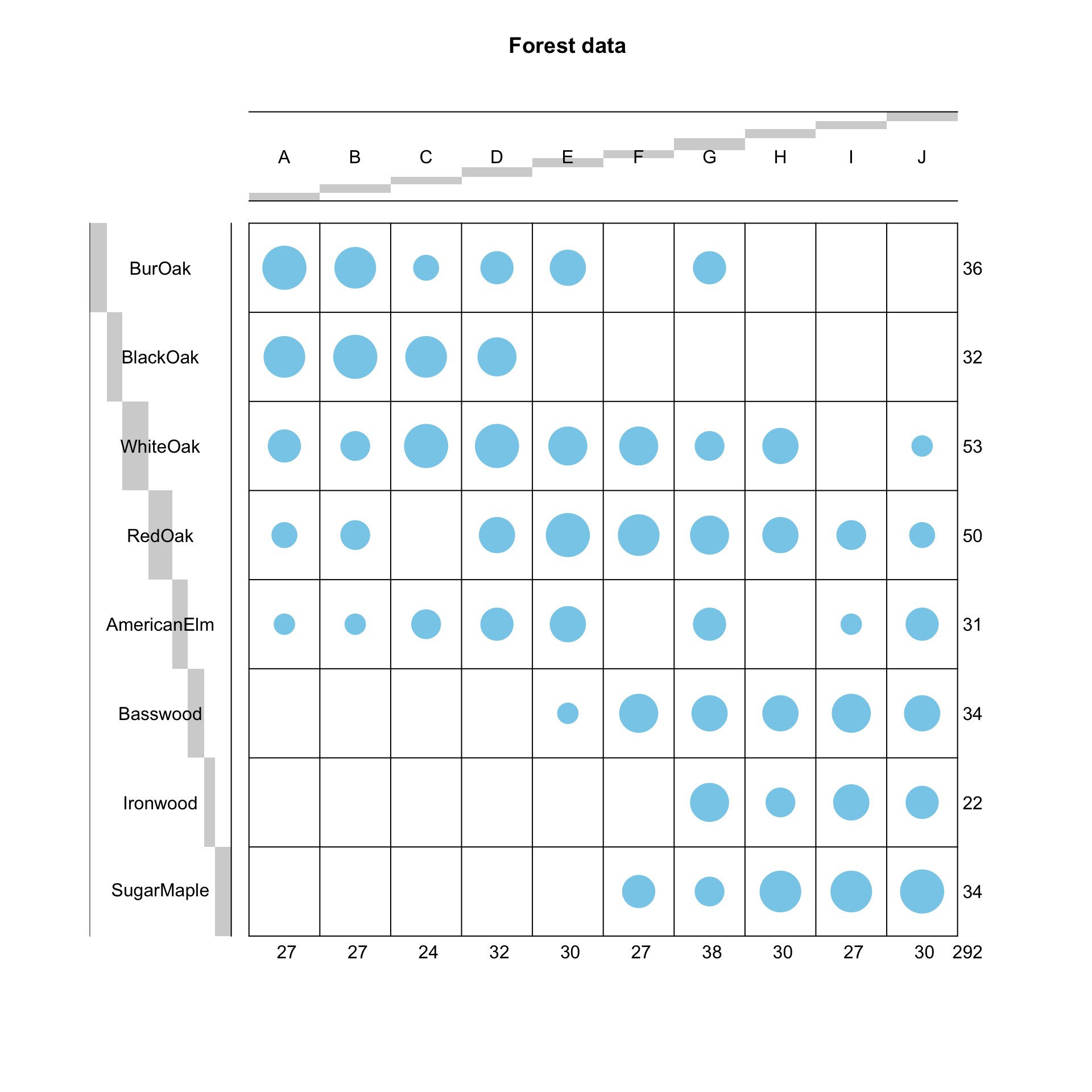
Task 1a
Check if there exists significant association between the rows and columns using Chi-square test. What is the total amount of the information contained in the data set (Hint: amount of information is the inertia, which can be obtained as \(\phi^{2} = \chi^{2}/\mbox{grand total}\))?
Click for solution
# chi-square test
dat <- forest_dat
chisq <- chisq.test(dat)
chisq##
## Pearson's Chi-squared test
##
## data: dat
## X-squared = 224.85, df = 63, p-value < 0.00000000000000022The p-value is very close to zero and is smaller than \(0.05\), so at the significance level of \(5\%\), we reject the null and it seems there exists an association between the row and the column.
# Total inertia
phi2 <- as.numeric(chisq$statistic/sum(dat))
phi2## [1] 0.7700459
Task 1b
Run the correspondence analysis by using CA() command. Based on the results, 1) extract the percentage of variance explained and 2) draw a scree plot using the command fviz_screeplot(). Based on examinations, determine the number of dimensions that can be used to represent the association in the data.
Click for solution
res <- CA(dat, graph=FALSE)
res$eig## eigenvalue percentage of variance cumulative percentage of variance
## dim 1 0.536732020 69.7013032 69.70130
## dim 2 0.096181795 12.4903978 82.19170
## dim 3 0.072097210 9.3627161 91.55442
## dim 4 0.045547474 5.9149038 97.46932
## dim 5 0.011065635 1.4370098 98.90633
## dim 6 0.004539267 0.5894801 99.49581
## dim 7 0.003882488 0.5041892 100.00000We can supplement this with a scree plot. Just look for the “elbow” as we did for PCA.
#scree plot
fviz_screeplot(res, addlabels = TRUE)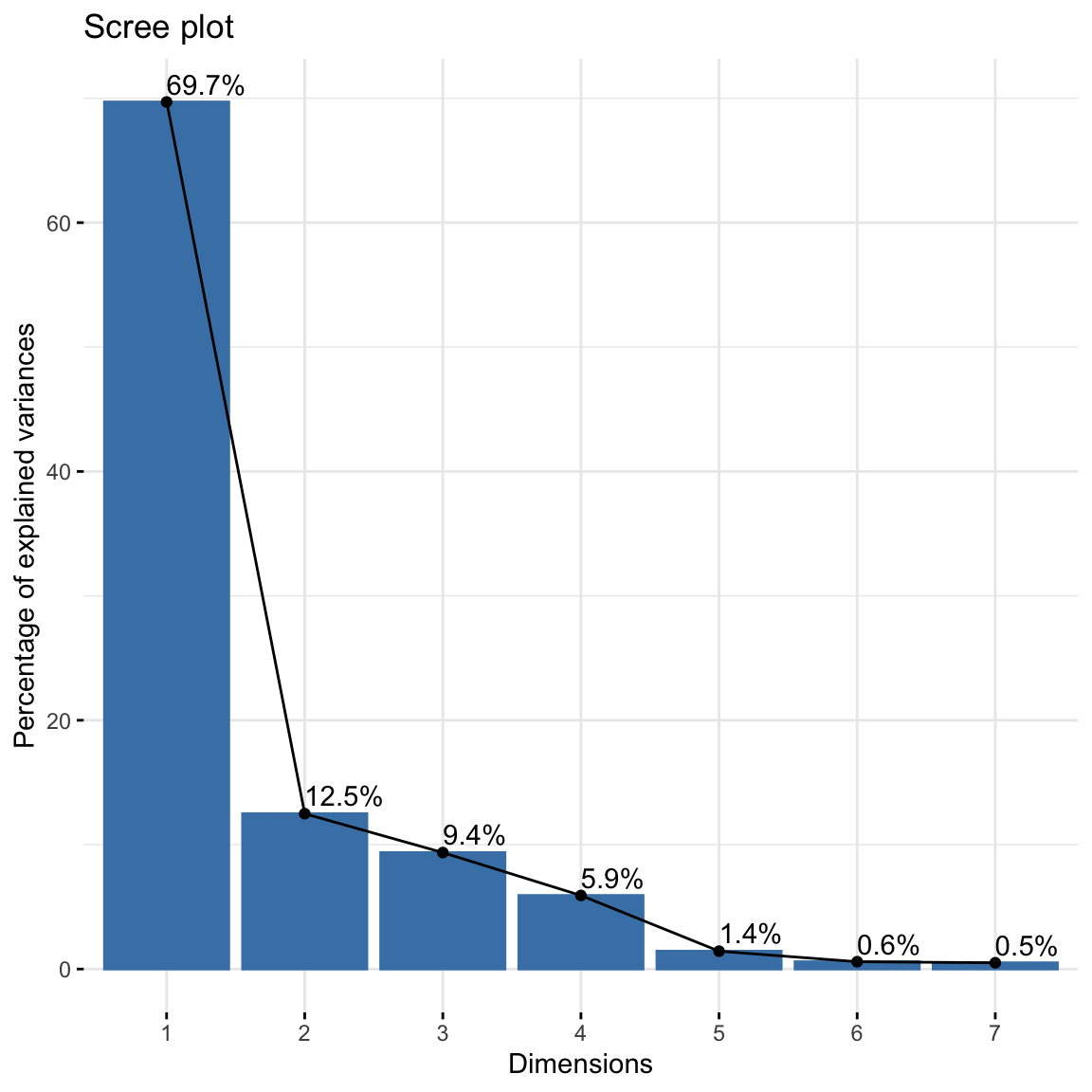
How many dimensions do you think is enough to preserve reasonable amount of variability? To have at least \(80\%\) of variations explained, we can go for 2 dimensions.
Task 1c
Extract the row and column coordinates from the results.
Click for solution
res$row$coord## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## BurOak 0.8146223 0.07340592 -0.3656428 0.27728345 0.011287524
## BlackOak 1.1788685 0.46701140 0.3309437 0.05964280 0.023447565
## WhiteOak 0.3436803 -0.28310606 0.2576998 -0.18141954 -0.108414950
## RedOak -0.1235665 -0.40336558 -0.1119886 0.16405319 0.013825790
## AmericanElm 0.1842648 0.01438946 -0.3519356 -0.46413156 0.134306791
## Basswood -0.8597898 -0.07549928 0.1162684 0.11671465 0.001282443
## Ironwood -0.9698189 0.54802045 -0.3162027 -0.07285919 -0.241365282
## SugarMaple -1.0067725 0.22501101 0.2478713 0.04542601 0.147086840res$col$coord## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## A 0.9341805 0.21494992 -0.054425848 0.28278501 0.0201338064
## B 0.9289734 0.24759385 -0.009334911 0.30496922 0.0674543646
## C 0.8931982 0.19694742 0.382075086 -0.42567165 -0.0859783259
## D 0.6653449 -0.12697131 0.043769437 -0.17061510 -0.0002006079
## E 0.2533103 -0.56279913 -0.406805727 -0.10638210 0.0765759116
## F -0.4870981 -0.55079395 0.408458894 0.18857423 0.0338399764
## G -0.3760968 0.06501352 -0.378830128 -0.01720966 -0.1757222461
## H -0.7175849 -0.06230205 0.284290270 0.10434288 -0.1104654143
## I -1.0119621 0.35528880 -0.034786432 0.08177379 0.0216169436
## J -0.8112801 0.28029409 -0.028901048 -0.22592714 0.1967270751
Task 1d
The first two dimensions can be used to plot row and column profiles using the code below
fviz_ca_row(res, repel = TRUE)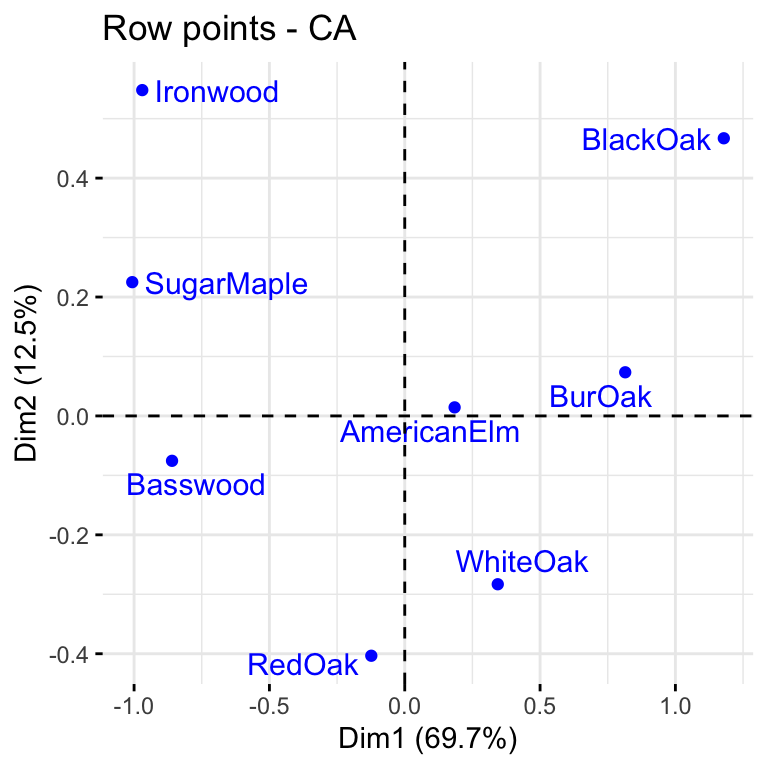
fviz_ca_col(res, repel = TRUE)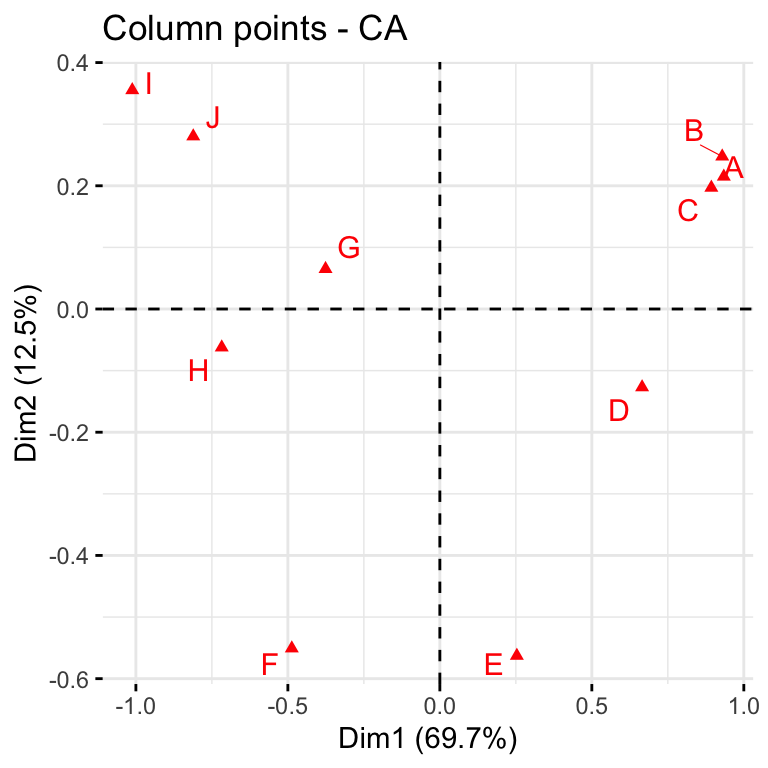 
We can use the code below to generate the symmetric biplot
fviz_ca_biplot(res, repel = TRUE) #"repel" away text from the data points.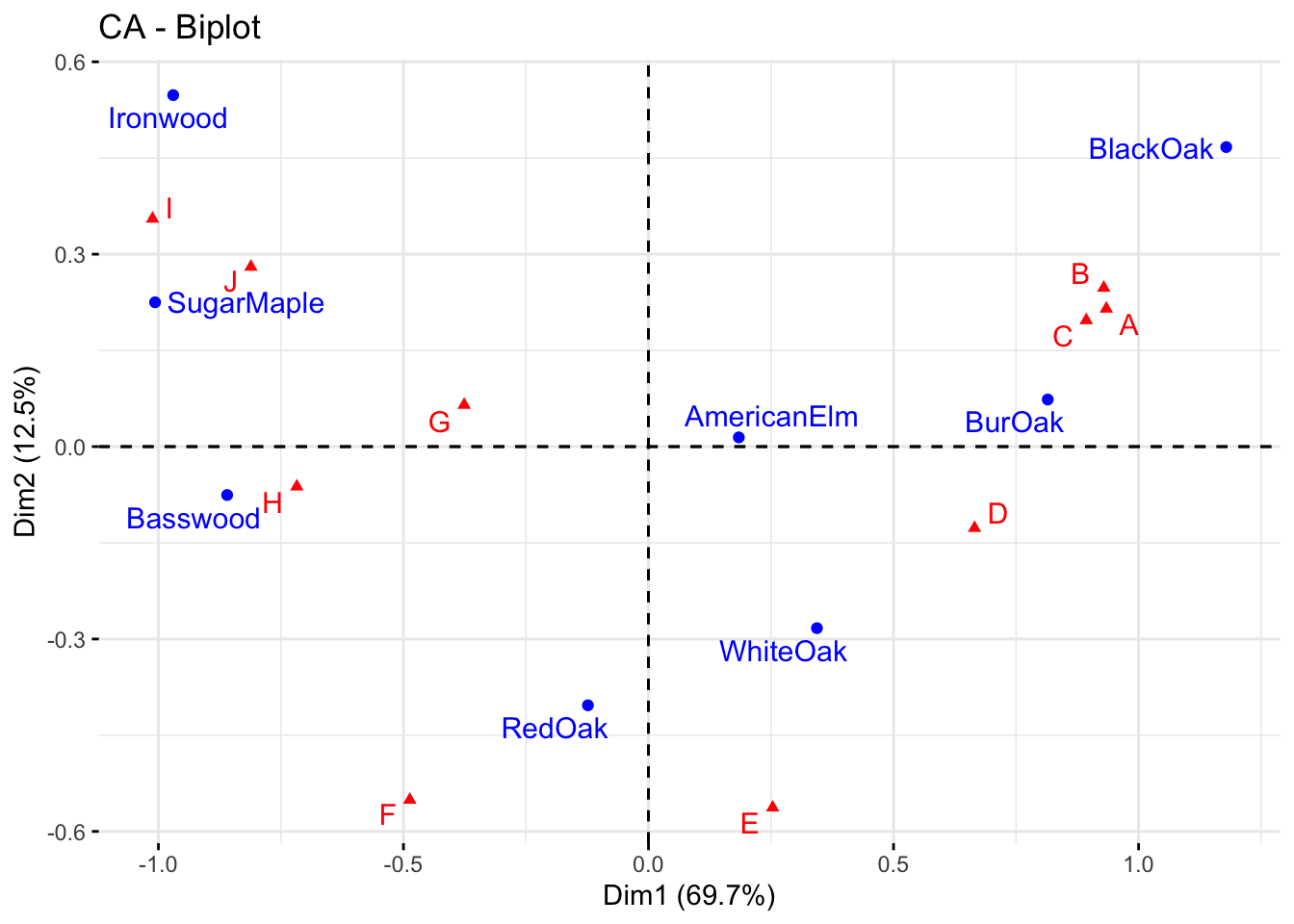
Explain the association between the trees and the sites.
Solutions to Task 1d
Click for solution
The distance between any row points (or column points) can be used as a measure of their similarity (e.g. row points with similar profiles are close to each other on the plot). From the plot, the sites A, B and C show similar pattern (distribution). Distance between any row and column profile is not meaningful, but we can just make a general statement about the pattern. For instance, sites A-E tend to relatively more oak species, while sites I, J, G tend to have more Ironwood and SugarMaple.
Task 1e
The asymmetric row biplot can be constructed using the following code:
fviz_ca_biplot(res,
map ="rowprincipal",
arrow=c(TRUE, TRUE),
repel = TRUE)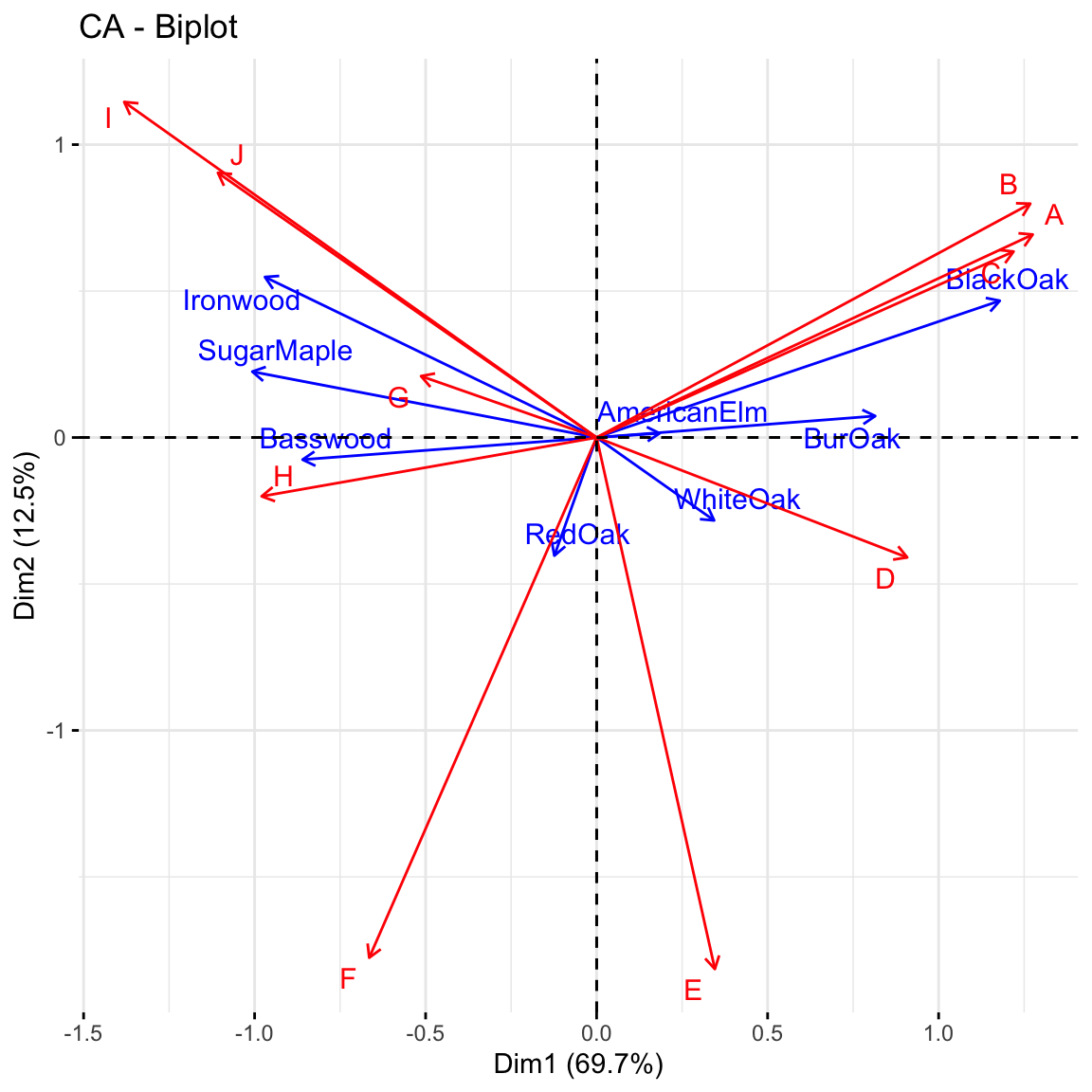
The contributions of rows to the first two dimensions can be plotted:
fviz_contrib(res, choice = "row", axes = 1:2)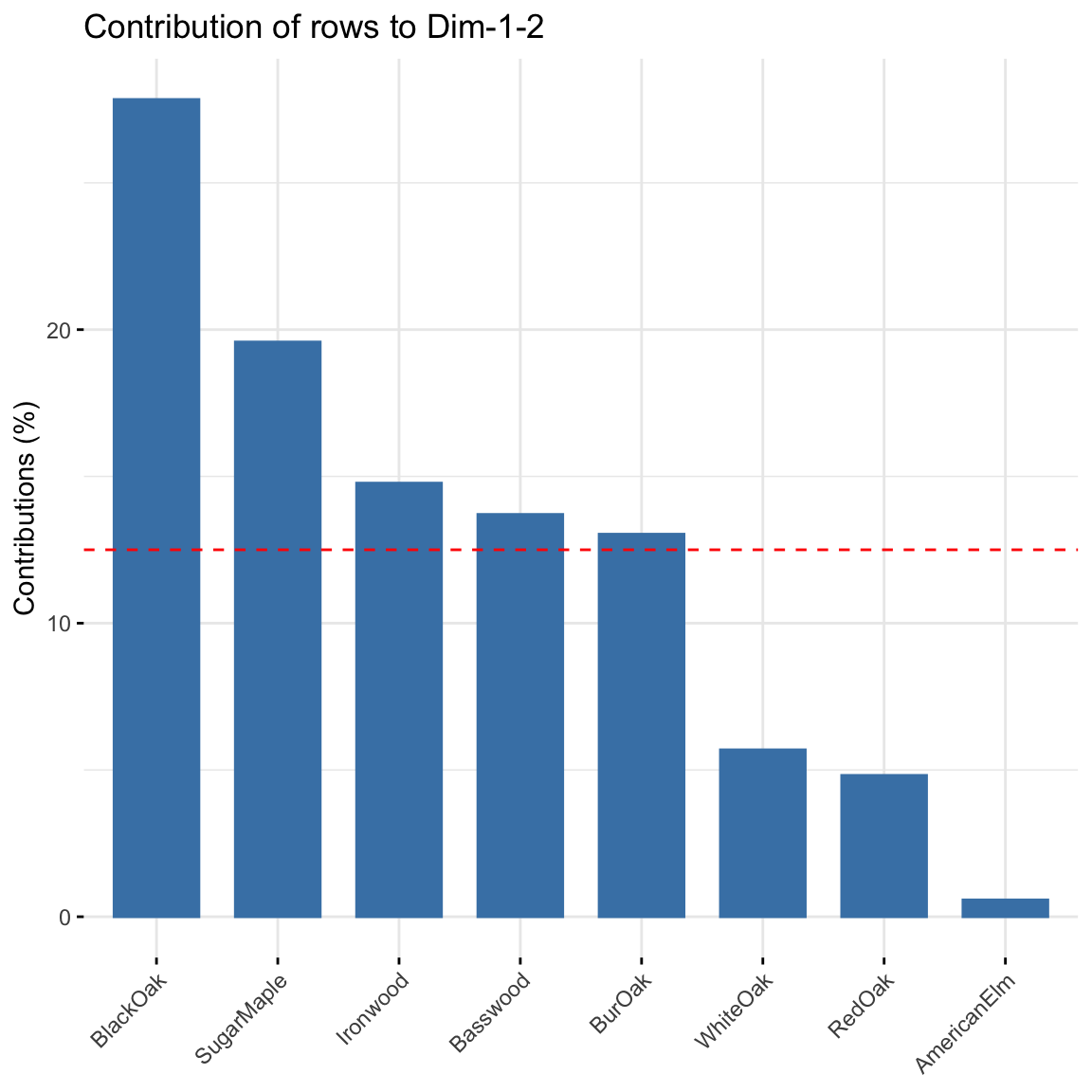
Run the codes given above and give a detailed explanation of the plots.
Click for solution
Asymmetric biplot: We can discuss the relationship between the row and column profiles with the asymmetric biplot. If the angle between a row and a column arrow is acute, then this indicates a strong association between the corresponding profiles. For instance, blackoak has a strong association with the sites A, B and C while Ironwood, SugarMaple and Basswood are more closely associated with the sites G, H, I and J. Revisit the ballon plot we made at the beginning of this practial and see if this interpretation agrees with it.
Contribution of rows: BlackOak contributed the most to both dimensions in explaining variability in the data while AmericanElm contributed the least. There are 8 trees, thus any distribution greater than 100/8 = 12.5% will contribute more to explaining the variability.
Task 1d
The quality of representation of the rows is called the squared cosine (cos2) or the squared correlations.
res$row$cos2[,1:2]## Dim 1 Dim 2
## BurOak 0.74638029 0.0060605181
## BlackOak 0.80402992 0.1261817120
## WhiteOak 0.37781669 0.2563718273
## RedOak 0.06732437 0.7174117897
## AmericanElm 0.08645636 0.0005272313
## Basswood 0.92865047 0.0071606634
## Ironwood 0.66853862 0.2134709480
## SugarMaple 0.87388999 0.0436517479Interpret this result.
Solution to Task 1d
Click for solution
Clearly Basswood, SugarMaple and BlackOak are highly correlated with dimension 1 but weakly associated with dimension 2. The opposite interpretation can be given for Redoak.
Exercise 2 (Analysis of House tasks data)
The dataset housetasks is available in the package factoextra (also available in ade4 package). The data is a contingency table containing 13 house tasks and their repartition in the couple: rows are the different tasks, values are the frequencies of the tasks done as follows:
by the wife only
alternatively
by the husband only
or jointly
We first call the data and the R packages needed.
library("FactoMineR")
library("factoextra")
data(housetasks)
head(housetasks)## Wife Alternating Husband Jointly
## Laundry 156 14 2 4
## Main_meal 124 20 5 4
## Dinner 77 11 7 13
## Breakfeast 82 36 15 7
## Tidying 53 11 1 57
## Dishes 32 24 4 53Task 2a
Perform the Chi-squre test to check the rows and the columns are independent.
Click for solution
library("FactoMineR")
library("factoextra")
data(housetasks)
head(housetasks)## Wife Alternating Husband Jointly
## Laundry 156 14 2 4
## Main_meal 124 20 5 4
## Dinner 77 11 7 13
## Breakfeast 82 36 15 7
## Tidying 53 11 1 57
## Dishes 32 24 4 53chisq <- chisq.test(housetasks)
chisq##
## Pearson's Chi-squared test
##
## data: housetasks
## X-squared = 1944.5, df = 36, p-value < 0.00000000000000022
Task 2b
Perform the correspondence analysis on this data and interpret the results. From the results, extract the amount of variability explained and draw a scree plot to decide the number of dimensions to use.
Click for solution
res.ca <- CA(housetasks, graph = FALSE)
res.ca## **Results of the Correspondence Analysis (CA)**
## The row variable has 13 categories; the column variable has 4 categories
## The chi square of independence between the two variables is equal to 1944.456 (p-value = 0 ).
## *The results are available in the following objects:
##
## name description
## 1 "$eig" "eigenvalues"
## 2 "$col" "results for the columns"
## 3 "$col$coord" "coord. for the columns"
## 4 "$col$cos2" "cos2 for the columns"
## 5 "$col$contrib" "contributions of the columns"
## 6 "$row" "results for the rows"
## 7 "$row$coord" "coord. for the rows"
## 8 "$row$cos2" "cos2 for the rows"
## 9 "$row$contrib" "contributions of the rows"
## 10 "$call" "summary called parameters"
## 11 "$call$marge.col" "weights of the columns"
## 12 "$call$marge.row" "weights of the rows"From res.ca one can extract appropriate quantity of interest for interpretation.
The amount of variability explained is as follows
eig.val <- res.ca$eig
eig.val## eigenvalue percentage of variance cumulative percentage of variance
## dim 1 0.5428893 48.69222 48.69222
## dim 2 0.4450028 39.91269 88.60491
## dim 3 0.1270484 11.39509 100.00000About 88.6% of the variation is explained by the first two dimensions. This is an acceptably large percentage. Alternatively scree plot can be used.
#screeplot
fviz_screeplot(res.ca, addlabels = TRUE)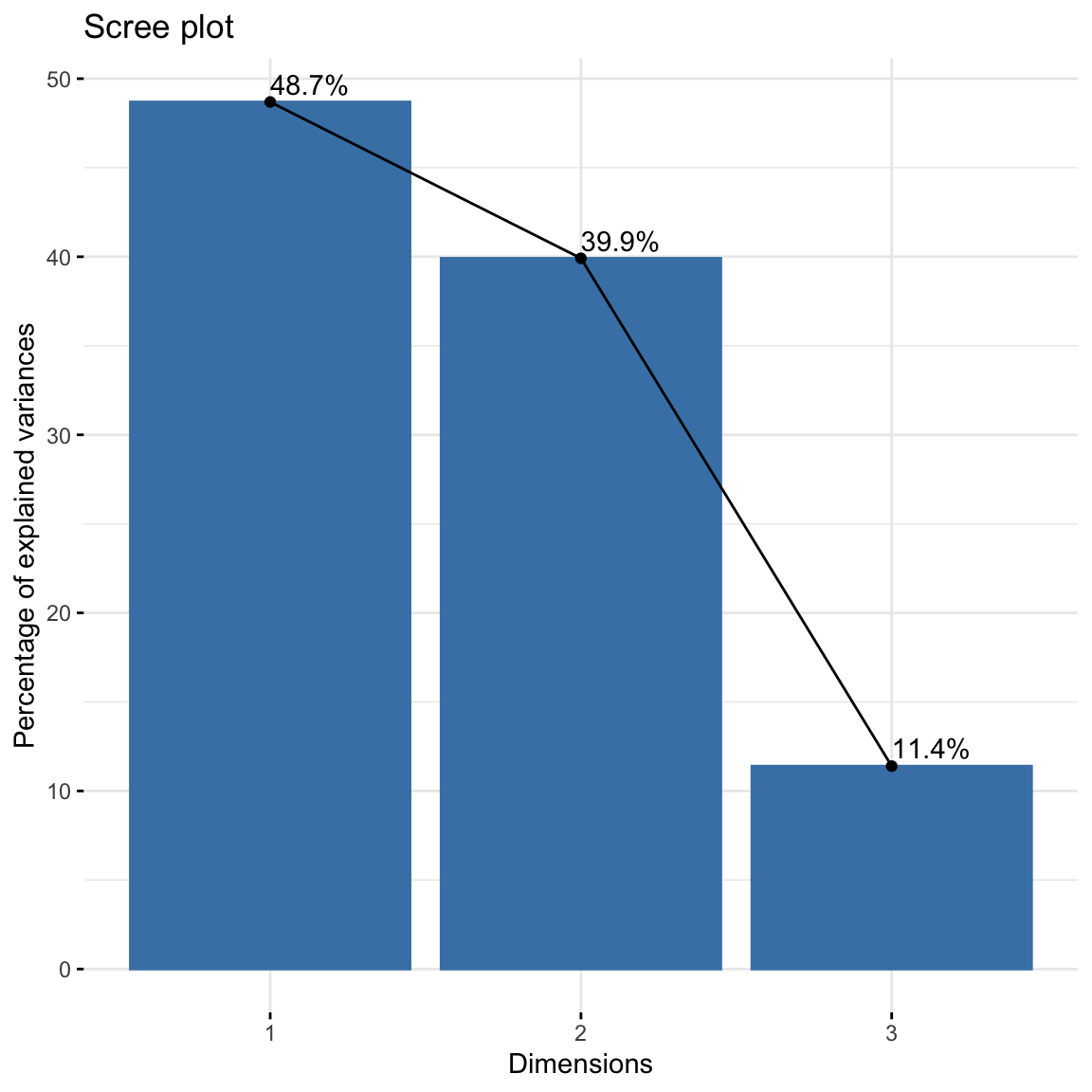
Task 2b
As done in the Forest data, generate the symmetric biplot, the contributions of columns and extract the squared cosine (cos2) and give appropriate explanations.
Click for solution
The symmetric biplot is as follows:
# repel= TRUE to avoid text overlapping (slow if many point)
fviz_ca_biplot(res.ca, repel = TRUE)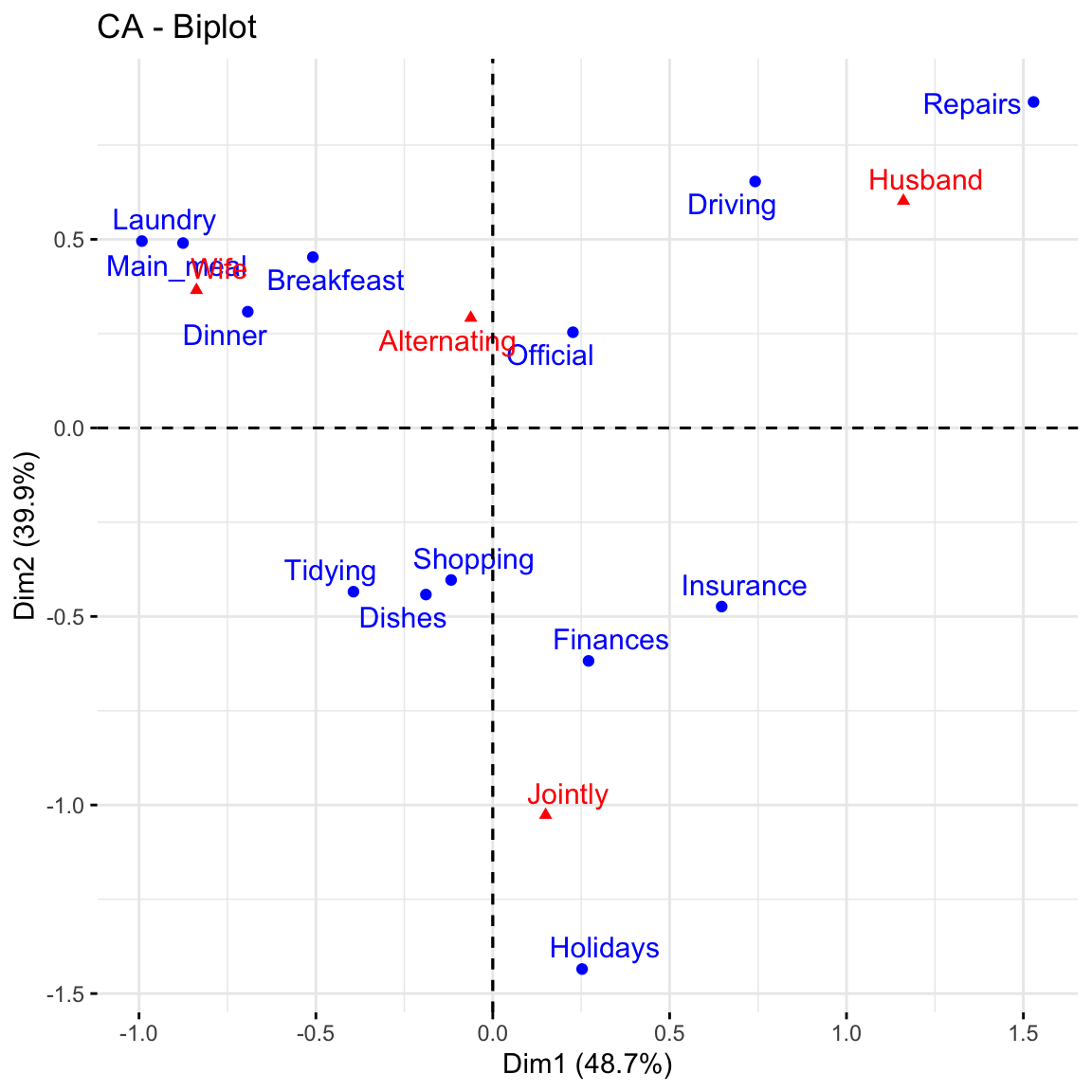
This graph shows that house tasks such as dinner, breakfeast, laundry are done more often by the wife while driving and repairs are done by the husband.
To visualize the contribution of columns to the first two dimensions, type this:
fviz_contrib(res.ca, choice = "col", axes = 1:2)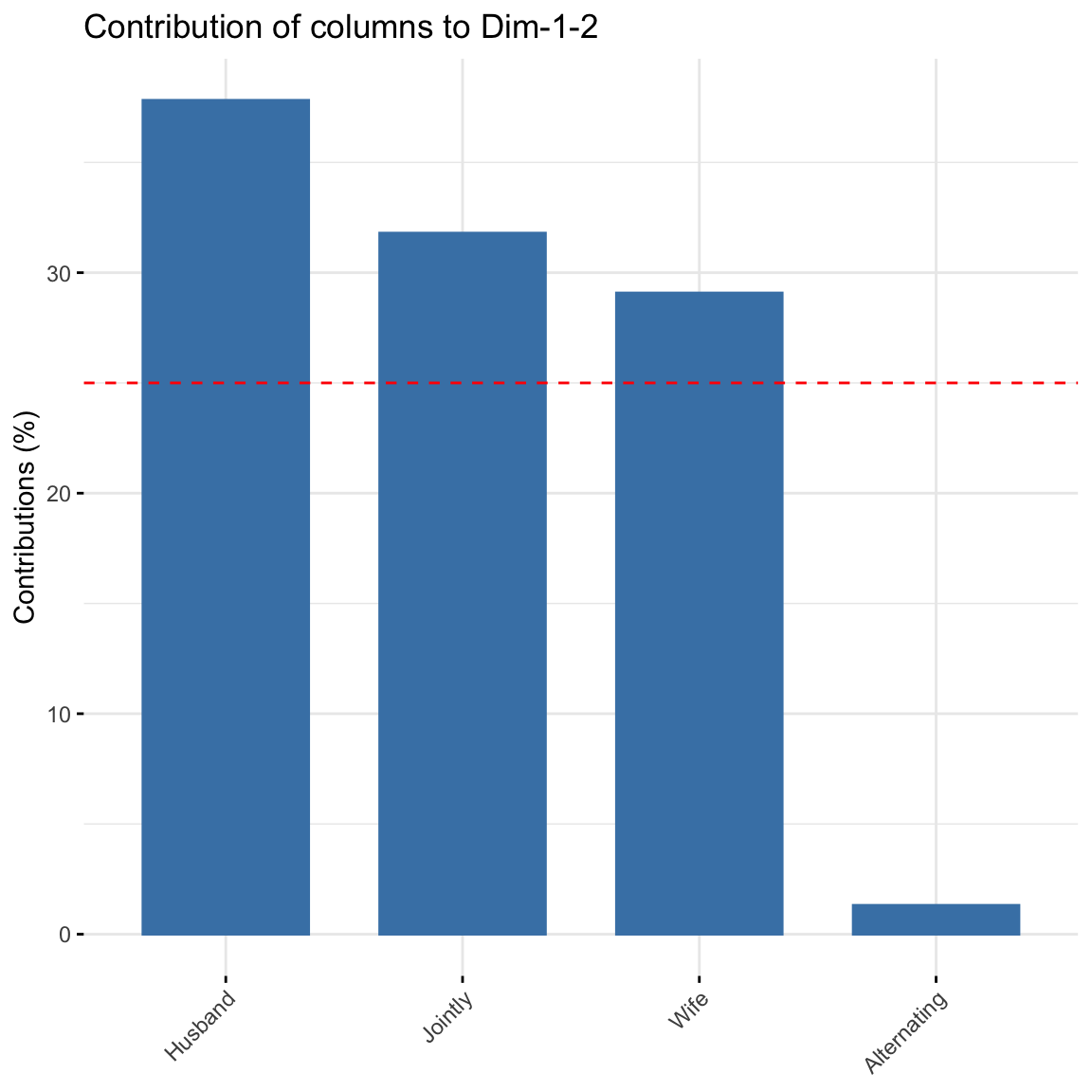
Alternating did not contribute much to explaining the variability in the data.
res.ca$row$cos2[,1:2]## Dim 1 Dim 2
## Laundry 0.73998741 0.18455213
## Main_meal 0.74160285 0.23235928
## Dinner 0.77664011 0.15370323
## Breakfeast 0.50494329 0.40023001
## Tidying 0.43981243 0.53501508
## Dishes 0.11811778 0.64615253
## Shopping 0.06365362 0.74765514
## Official 0.05304464 0.06642648
## Driving 0.43201860 0.33522911
## Finances 0.16067678 0.83666958
## Insurance 0.57601197 0.30880208
## Repairs 0.70673575 0.22587147
## Holidays 0.02979239 0.96235977Dinner, Main_meal, Laundry and Repairs are highly correlated with dimension 1 while Holidays, Finances and Shopping are highly correlated with dimension 2.