Lab 2: Principal Component Analysis

This computer practical consists of three exercises; first we use factorextra package to visualise the results obtained by principal component analysis, and then we examine how the strength of existing redendancy in data affects the PCA results. In exercise 3, we will get a taste of principal component regression.

Exercise 1 (Iris data)

Here we use the same data (Iris data) illustrated in the Workshop, but will use the different function to perform PCA. First load the following package(s) into your workspace for visualisation

library(factoextra)

Task 1a

Use prcomp() to perfrom the PCA. For this run ?prcomp first. Check if the output of PCA agrees with the results obtained by running the command eigen() in the Workshop:PCA. Where do you get the eigenvalues, PC loadings and PC scores here?

Solution to Task 1

Click for solution

pr.out <- prcomp(iris[,-5] , scale =TRUE)
names(pr.out)
summary(pr.out)

# eigenvalues
pr.out$sdev^2

# PC loadings
pr.out$rotation

# PC score
pr.out$x

Task 1b

How do you interpret the Standard deviation of the principal components from the summary table? Can you manually compute the Proportion of Variance of the PC1 to PC4 by using the Standard deviation of the principal components?

Solution to Task 1b

Click for solution

The Standard deviation of the principal components is the square root of the corresponding eigenvalues.

sd_all <- summary(pr.out)$importance[1,]
sd_all^2/sum(sd_all^2)

##         PC1         PC2         PC3         PC4 
## 0.729624454 0.228507618 0.036689219 0.005178709

summary(pr.out)$importance[2,]

##     PC1     PC2     PC3     PC4 
## 0.72962 0.22851 0.03669 0.00518

Type the following code to make a scree plot:

library(factoextra)
fviz_screeplot(pr.out, addlabels = TRUE)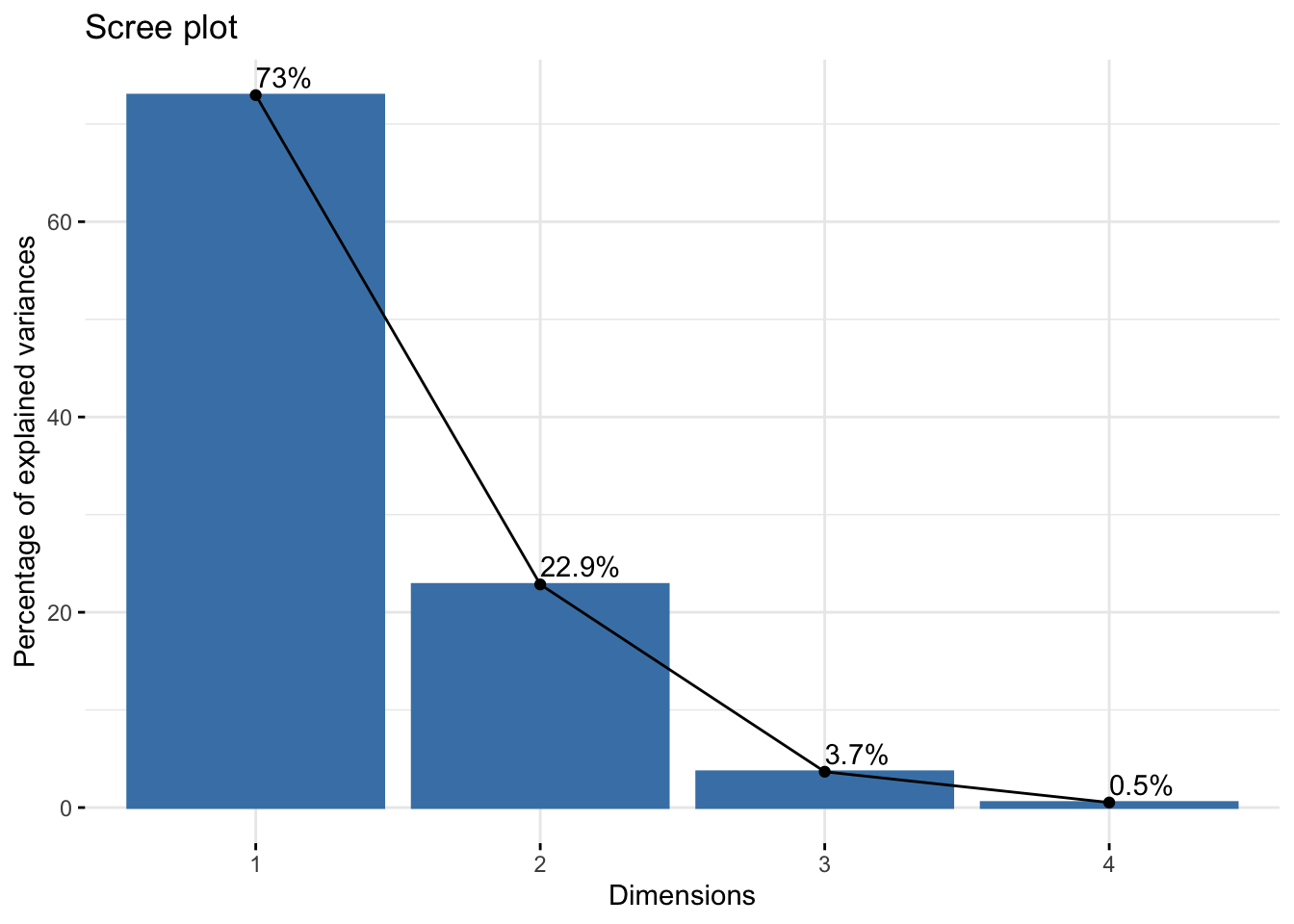

Correlation between variables and PCs, quality of representation (cos2) and contributions can be obtained respectively as

var <- get_pca_var(pr.out)
var$cor

##                   Dim.1       Dim.2       Dim.3       Dim.4
## Sepal.Length  0.8901688 -0.36082989  0.27565767  0.03760602
## Sepal.Width  -0.4601427 -0.88271627 -0.09361987 -0.01777631
## Petal.Length  0.9915552 -0.02341519 -0.05444699 -0.11534978
## Petal.Width   0.9649790 -0.06399985 -0.24298265  0.07535950

var$cos2

##                  Dim.1       Dim.2       Dim.3        Dim.4
## Sepal.Length 0.7924004 0.130198208 0.075987149 0.0014142127
## Sepal.Width  0.2117313 0.779188012 0.008764681 0.0003159971
## Petal.Length 0.9831817 0.000548271 0.002964475 0.0133055723
## Petal.Width  0.9311844 0.004095980 0.059040571 0.0056790544

var$contrib

##                  Dim.1       Dim.2     Dim.3     Dim.4
## Sepal.Length 27.150969 14.24440565 51.777574  6.827052
## Sepal.Width   7.254804 85.24748749  5.972245  1.525463
## Petal.Length 33.687936  0.05998389  2.019990 64.232089
## Petal.Width  31.906291  0.44812296 40.230191 27.415396

Run the code above and check to see that these values are in agreement with the results in the step-by-step approach in the tutorials.

You can plot the contribution of the variables to PC1 as follows:

fviz_contrib(pr.out, choice = "var", axes = 1, top = 10)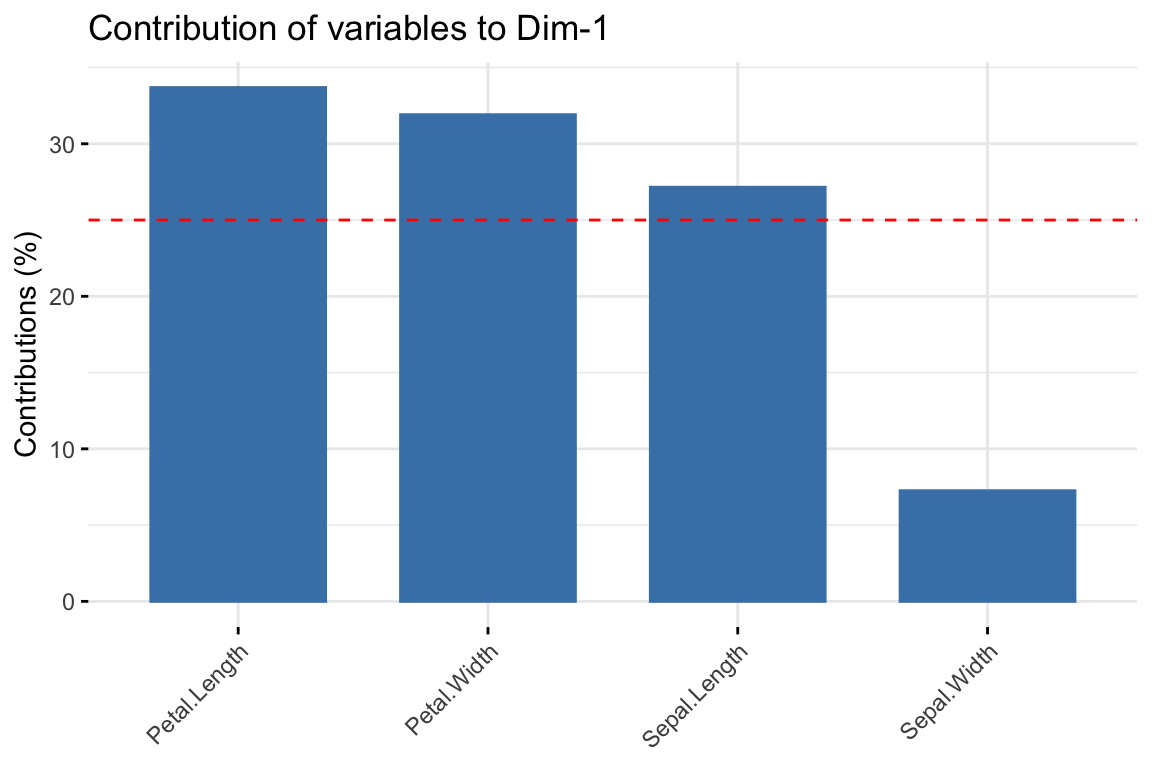

Task 1c

Modify the code to plot the contribution of the variables to PC2.

Solution to Task 1c

Click for solution

# Contributions of variables to PC2
fviz_contrib(pr.out, choice = "var", axes = 2, top = 10)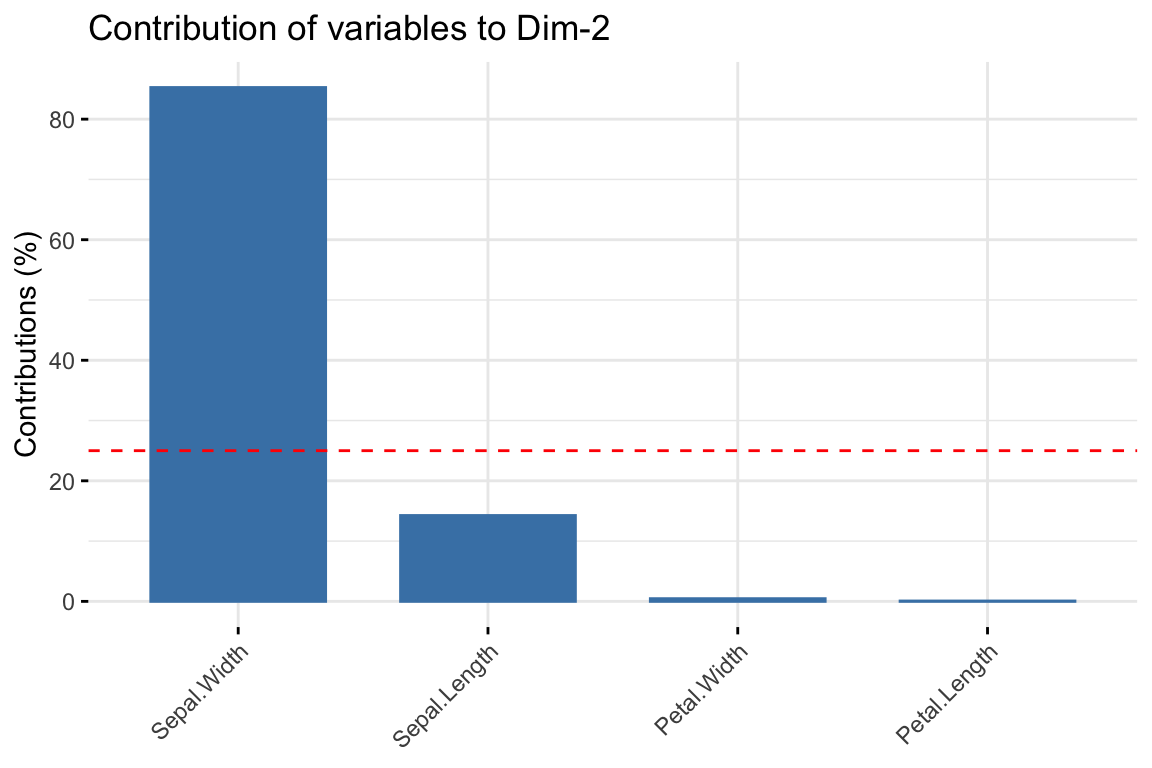

There are various ways to make a biplot. Try the following codes:

biplot (pr.out , scale =0)
abline(h=0, col="gray",lty=3, lwd =2)
abline(v=0, col="gray",lty=3, lwd =2)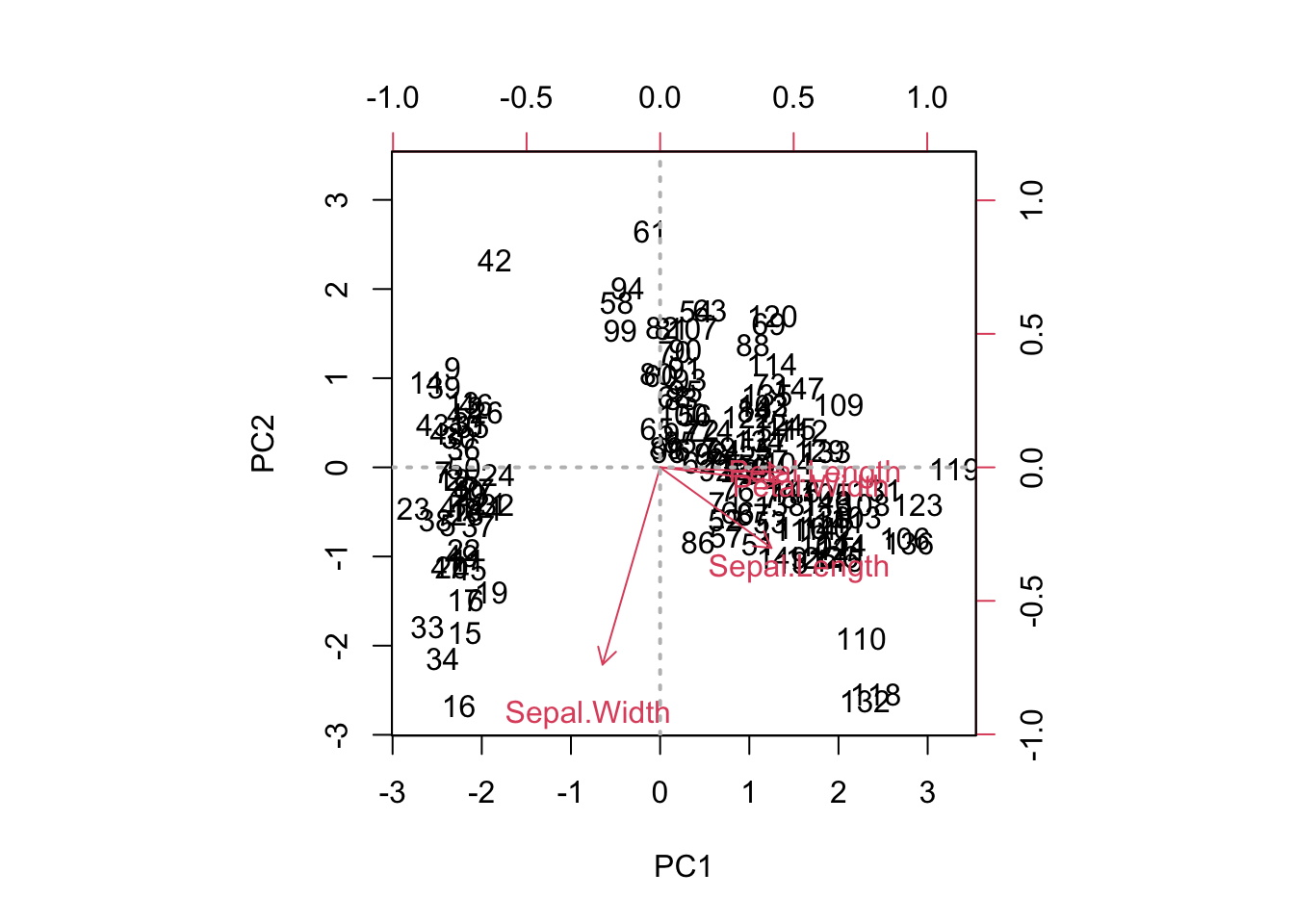

and a more elegant one.

fviz_pca_biplot(pr.out,
                col.ind = iris$Species, palette = "jco",
                addEllipses = TRUE, label = "var",
                col.var = "black", repel = TRUE,
                legend.title = "Species")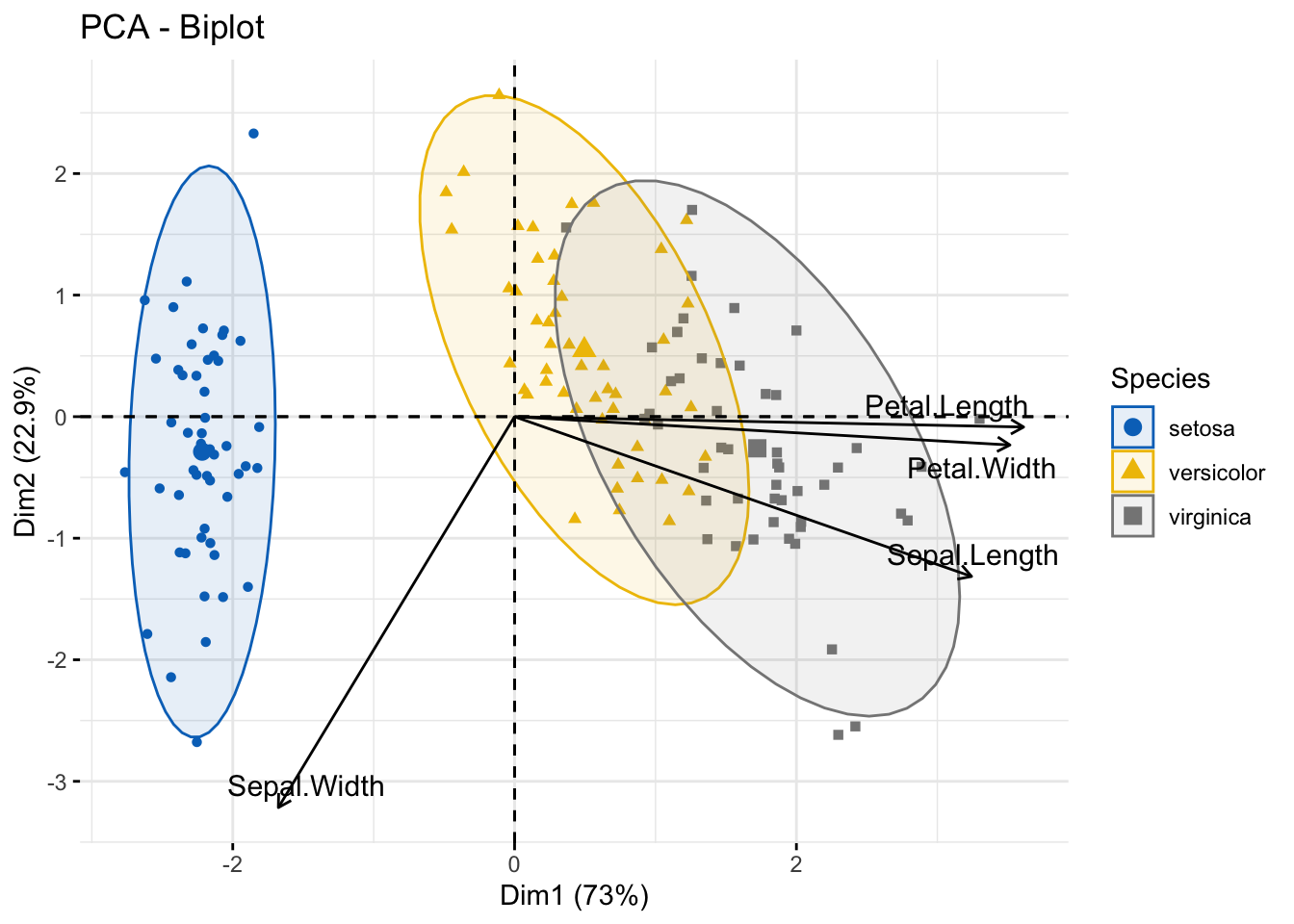

You can obtain alternative visualisation of a biplot using autoplot function in the ggfortifyCheck package (please check these out at your own convenience).

Exercise 2

Generate n = 200 observations and p=30 variables from a multivariate normal distribution with correlation matrix given as \(corr(x_{i},x_{j}) = \rho^{|i-j|}\). You can create the covariance matrix using

covmat <- function(rho, p) {
  rho^(abs(outer(seq(p), seq(p), "-")))
}

and use the mvrnorm function in MASS package to generate the multivariate Gaussian data.

Task 2a

Take \(\rho=0.95\) and carry out PCA. For reproducibility, take the pseudo-number generator, seed =123. How many PCs is sufficient for this data? Comment on your general observation. (Hint: Use the following codes to generate the data called dd.

library(MASS)
set.seed(123)
p = 30
n = 200
cov.e = covmat(0.95, p)
mean.e = rep(0, p)
dd <- mvrnorm(n, mean.e, cov.e)

Solution to Task 2a

Click for solution

prr <- prcomp(dd)
summary(prr)

## Importance of components:
##                           PC1    PC2    PC3     PC4     PC5     PC6     PC7
## Standard deviation     4.1415 2.2933 1.3464 1.00341 0.77935 0.63838 0.48520
## Proportion of Variance 0.6179 0.1895 0.0653 0.03627 0.02188 0.01468 0.00848
## Cumulative Proportion  0.6179 0.8073 0.8726 0.90886 0.93074 0.94542 0.95390
##                            PC8     PC9    PC10    PC11    PC12    PC13   PC14
## Standard deviation     0.41615 0.40216 0.37139 0.29564 0.29060 0.26536 0.2469
## Proportion of Variance 0.00624 0.00583 0.00497 0.00315 0.00304 0.00254 0.0022
## Cumulative Proportion  0.96014 0.96597 0.97093 0.97408 0.97712 0.97966 0.9819
##                           PC15    PC16    PC17    PC18    PC19    PC20    PC21
## Standard deviation     0.24380 0.22571 0.21583 0.20360 0.18959 0.18087 0.17804
## Proportion of Variance 0.00214 0.00184 0.00168 0.00149 0.00129 0.00118 0.00114
## Cumulative Proportion  0.98400 0.98583 0.98751 0.98900 0.99030 0.99148 0.99262
##                          PC22    PC23    PC24    PC25    PC26    PC27   PC28
## Standard deviation     0.1744 0.16711 0.16001 0.15574 0.15240 0.14561 0.1390
## Proportion of Variance 0.0011 0.00101 0.00092 0.00087 0.00084 0.00076 0.0007
## Cumulative Proportion  0.9937 0.99472 0.99564 0.99652 0.99735 0.99812 0.9988
##                           PC29    PC30
## Standard deviation     0.12848 0.12825
## Proportion of Variance 0.00059 0.00059
## Cumulative Proportion  0.99941 1.00000

plot(summary(prr)$importance[2,], type="b", xlab="PCs", ylab="Variability explained")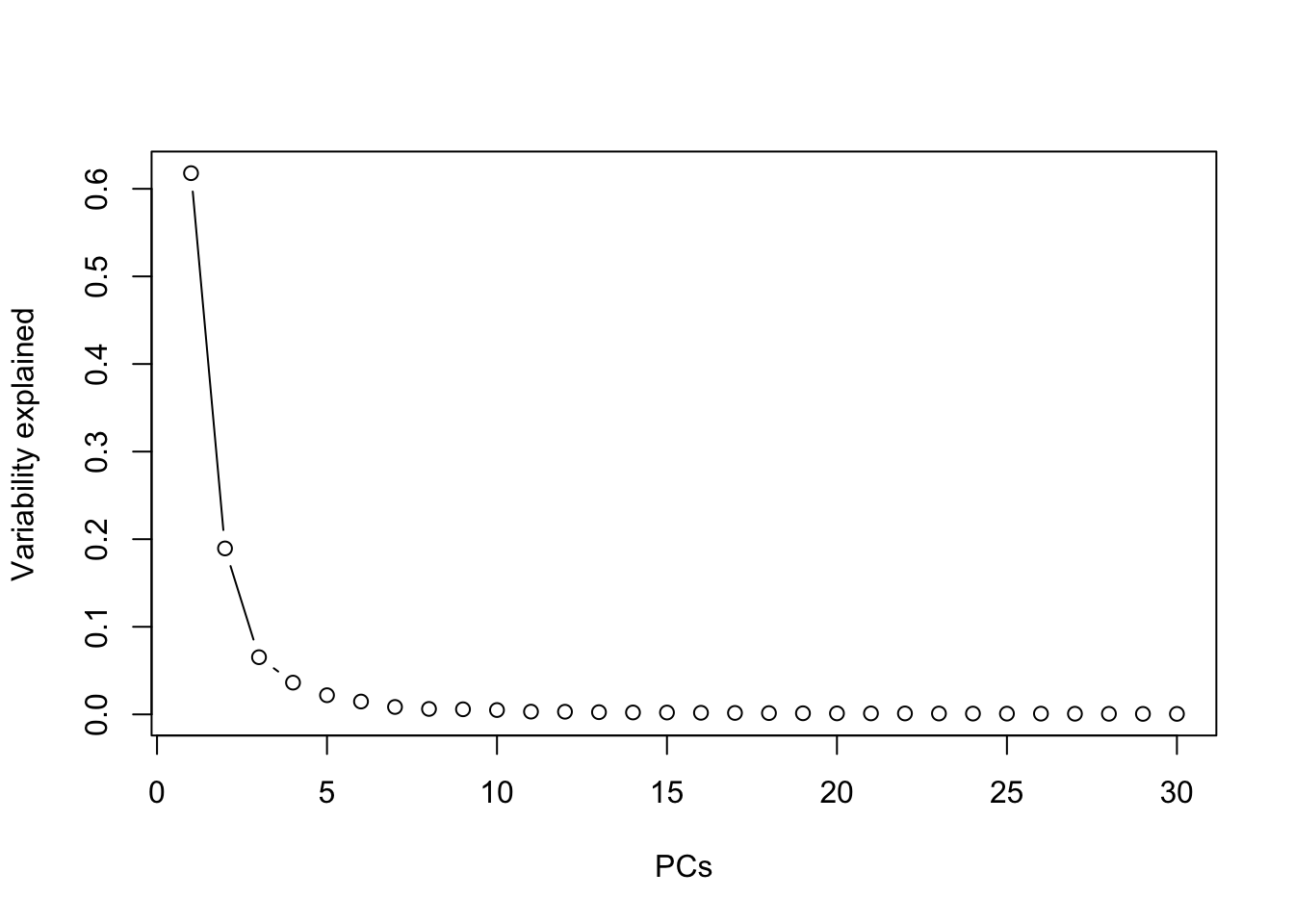

The summary shows that 2 components are enough to keep 80% of the variability in data. Also choosing 2 principal components seems reasonable based on the so-called elbow method.

Task 2b

Take \(\rho=0.2\) and carry out PCA. As done before, use the pseudo-number generator, seed = 123 for reproducibility. How many PCs are sufficient for this data? Compare your results with the case of \(\rho=0.95\).

Solution to task 2b

Click for solution

library(MASS)
set.seed(123)
p = 30
n = 200
cov.e = covmat(0.2, p)
mean.e = rep(0, p)
dd <- mvrnorm(n, mean.e, cov.e)

prr <- prcomp(dd)
summary(prr)

## Importance of components:
##                            PC1     PC2     PC3     PC4     PC5     PC6     PC7
## Standard deviation     1.46267 1.33775 1.32938 1.28976 1.22917 1.17781 1.17183
## Proportion of Variance 0.07223 0.06042 0.05966 0.05616 0.05101 0.04683 0.04636
## Cumulative Proportion  0.07223 0.13265 0.19231 0.24847 0.29948 0.34631 0.39267
##                            PC8     PC9   PC10    PC11    PC12    PC13    PC14
## Standard deviation     1.16283 1.13430 1.1074 1.05365 1.03779 1.01332 0.99861
## Proportion of Variance 0.04565 0.04344 0.0414 0.03748 0.03636 0.03467 0.03367
## Cumulative Proportion  0.43832 0.48176 0.5232 0.56065 0.59701 0.63167 0.66534
##                           PC15    PC16    PC17    PC18    PC19    PC20    PC21
## Standard deviation     0.96032 0.92220 0.91021 0.88108 0.85584 0.83619 0.81532
## Proportion of Variance 0.03114 0.02871 0.02797 0.02621 0.02473 0.02361 0.02244
## Cumulative Proportion  0.69648 0.72519 0.75316 0.77937 0.80410 0.82770 0.85015
##                           PC22    PC23    PC24    PC25    PC26    PC27    PC28
## Standard deviation     0.78841 0.75942 0.74078 0.71840 0.70589 0.69243 0.66375
## Proportion of Variance 0.02099 0.01947 0.01853 0.01742 0.01682 0.01619 0.01487
## Cumulative Proportion  0.87113 0.89060 0.90913 0.92655 0.94338 0.95956 0.97444
##                           PC29    PC30
## Standard deviation     0.62502 0.60544
## Proportion of Variance 0.01319 0.01238
## Cumulative Proportion  0.98762 1.00000

plot(summary(prr)$importance[2,], type="b", xlab="PCs", ylab="Variability explained")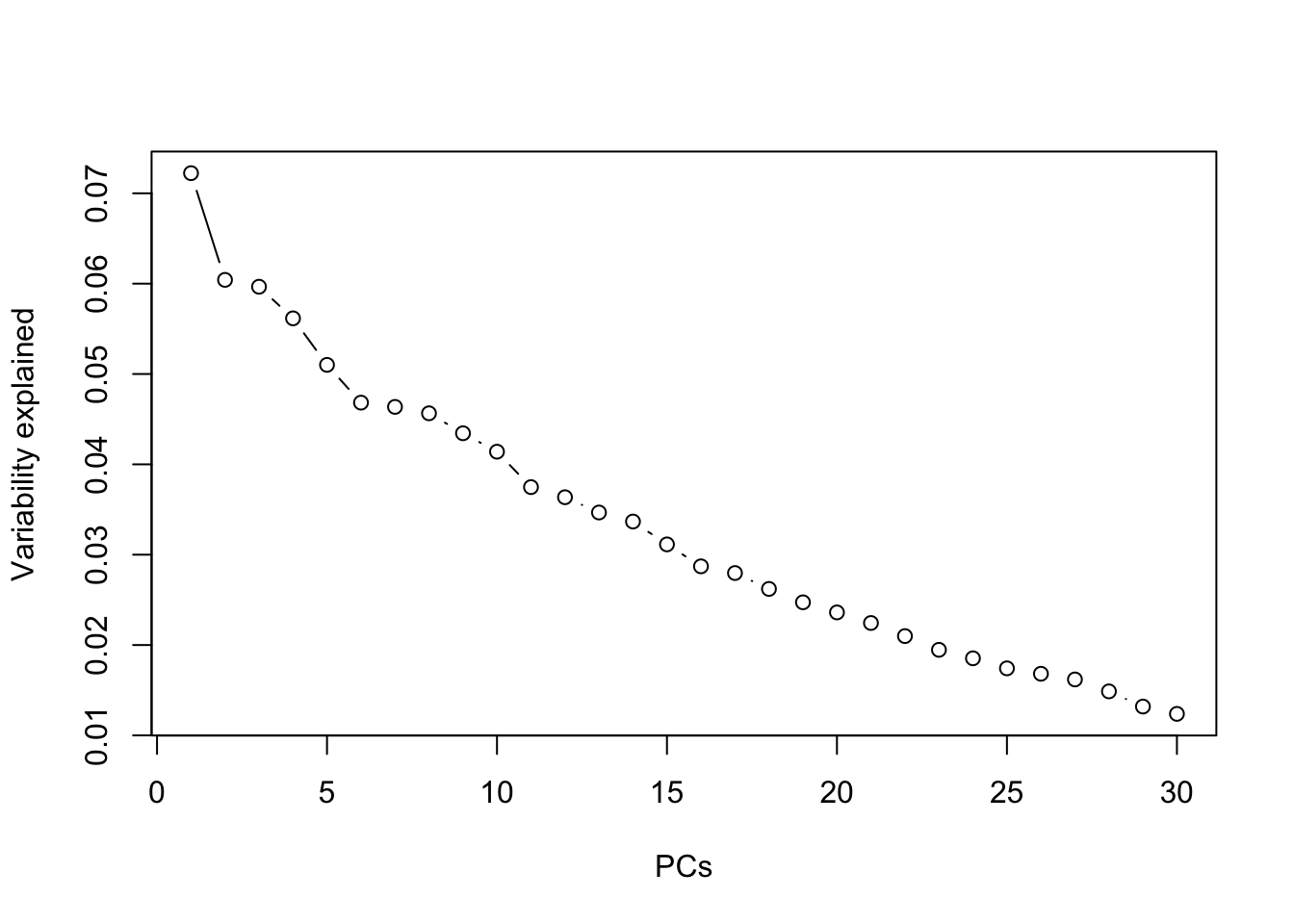

The summary shows that 19 components are enough to keep 80% of the variability in data. This shows that the higher the correlation, the higher the redundancy in the data in which case PCA becomes more useful and gives more clear interpretation.

Exercise 3

One of the many uses of PCA is principal component regression (PCR). We have seen that Sepal length is highly correlated with Petal length and Petal width.

Task 3a

Suppose that we want to carryout regression analysis between Sepal length (response variable) and the three remaining variables (covariates). Then we can use PCA to reduce the correlation. Perform the PCA and find the principal scores.

Solution to task 3a

Click for solution

iris.pca <- prcomp(iris[,2:4], scale=TRUE)
iris.pca$x

##               PC1          PC2          PC3
##   [1,] -2.1248387 -0.139743260  0.008370721
##   [2,] -1.6451988  0.900407772 -0.054584971
##   [3,] -1.8737775  0.498821958 -0.070033694
##   [4,] -1.7044039  0.677902966 -0.001362832
##   [5,] -2.2207666 -0.347773466  0.020961859
##   [6,] -2.2314161 -1.103311779 -0.001635822
##   [7,] -1.9454276  0.024274998 -0.095352466
##   [8,] -1.9921879  0.053812348  0.036410583
##   [9,] -1.5492708  1.108437978 -0.067176109
##  [10,] -1.7878870  0.721914915  0.089769216
##  [11,] -2.2799718 -0.570278271  0.074183997
##  [12,] -1.9554651  0.039337749  0.077041583
##  [13,] -1.7286818  0.944419721  0.036547077
##  [14,] -1.8388502  0.987843518 -0.085345923
##  [15,] -2.6779242 -1.150945093 -0.009935588
##  [16,] -2.7845016 -2.114513613 -0.019942131
##  [17,] -2.3783073 -1.045413383 -0.164159822
##  [18,] -2.0413556 -0.183755209 -0.082761327
##  [19,] -2.2189712 -0.851269624  0.076905088
##  [20,] -2.2924168 -0.822320426 -0.004356912
##  [21,] -1.9187423  0.024863150  0.117672583
##  [22,] -2.1130058 -0.658302169 -0.108080099
##  [23,] -2.3676579 -0.289875070 -0.141562142
##  [24,] -1.5723652  0.100857509 -0.168314699
##  [25,] -1.8452967 -0.004086048  0.198934583
##  [26,] -1.5717531  0.871458574  0.026677030
##  [27,] -1.7884990 -0.048686149 -0.105222513
##  [28,] -2.0881159 -0.154217859  0.049001721
##  [29,] -2.0289107  0.068286947 -0.004220418
##  [30,] -1.7636091  0.455398161  0.051859306
##  [31,] -1.6676811  0.663428368  0.039268168
##  [32,] -1.8252218 -0.034211550 -0.145853513
##  [33,] -2.7471668 -1.358387147  0.215680599
##  [34,] -2.7963345 -1.595954703  0.096508689
##  [35,] -1.7044039  0.677902966 -0.001362832
##  [36,] -1.9105003  0.513296557 -0.110664695
##  [37,] -2.1615615 -0.125268661 -0.032260280
##  [38,] -2.3042497 -0.303761517  0.112093907
##  [39,] -1.6819216  0.914882371 -0.095215971
##  [40,] -1.9921879  0.053812348  0.036410583
##  [41,] -2.0780784 -0.169280610 -0.123392328
##  [42,] -0.9269427  2.327081865 -0.274485987
##  [43,] -1.8737775  0.498821958 -0.070033694
##  [44,] -1.7174609 -0.344740253 -0.274895471
##  [45,] -2.0620425 -0.924230771  0.067035040
##  [46,] -1.5617157  0.856395823 -0.145717019
##  [47,] -2.3391770 -0.792783076  0.127406136
##  [48,] -1.8370547  0.484347359 -0.029402694
##  [49,] -2.2799718 -0.570278271  0.074183997
##  [50,] -1.9329827  0.276317153 -0.016811556
##  [51,]  0.3765942 -0.521457794  0.217835736
##  [52,]  0.3866316 -0.536520545  0.045441688
##  [53,]  0.6294508 -0.386388735  0.195374550
##  [54,]  0.8994033  1.496148204 -0.088769462
##  [55,]  0.8070663  0.281125681  0.035708135
##  [56,]  0.6033775  0.383624178  0.177341231
##  [57,]  0.4476323 -0.817511898  0.048162778
##  [58,]  0.2959666  1.521476037 -0.087199181
##  [59,]  0.5441723  0.161119373  0.230563369
##  [60,]  0.5624516  0.634490029 -0.170167957
##  [61,]  0.7531242  2.324647664 -0.056301734
##  [62,]  0.4683191 -0.077036336 -0.101633589
##  [63,]  0.7448822  1.836214257  0.172035544
##  [64,]  0.6643781  0.102632825  0.180062321
##  [65,]  0.1769442  0.305865362 -0.175746633
##  [66,]  0.3623537 -0.270003791  0.083351597
##  [67,]  0.5784876 -0.120460133  0.020259411
##  [68,]  0.3019651  0.781588627  0.275622236
##  [69,]  1.3459114  1.543781517 -0.080469695
##  [70,]  0.5038585  1.182586288  0.078045911
##  [71,]  0.7472491 -0.711980189 -0.106061456
##  [72,]  0.4197634  0.455997173 -0.025813770
##  [73,]  1.2050187  0.861792503  0.119827721
##  [74,]  0.5933400  0.398686929  0.349735279
##  [75,]  0.4340039  0.204543170  0.108670369
##  [76,]  0.4582817 -0.061973585  0.070760459
##  [77,]  0.7970289  0.296188432  0.208102183
##  [78,]  0.9290676 -0.280857025  0.041150316
##  [79,]  0.6744155  0.087570074  0.007668273
##  [80,]  0.1775563  1.076466427  0.019245096
##  [81,]  0.5630637  1.405091093  0.024823772
##  [82,]  0.4428579  1.463577641  0.075324820
##  [83,]  0.3954856  0.722513927  0.012096139
##  [84,]  1.1700913  0.372770943  0.135139949
##  [85,]  0.5784876 -0.120460133  0.020259411
##  [86,]  0.2782587 -0.996592907 -0.020508084
##  [87,]  0.5560052 -0.357439537  0.114112550
##  [88,]  1.0462946  1.438249808  0.073754539
##  [89,]  0.2646303  0.025462161  0.039999506
##  [90,]  0.7075474  1.080087791 -0.063587185
##  [91,]  0.6750276  0.858171138  0.202660002
##  [92,]  0.5317273 -0.090922783  0.152022459
##  [93,]  0.5281364  0.916069534  0.040136001
##  [94,]  0.3918946  1.729506244 -0.099790319
##  [95,]  0.5891370  0.635078181  0.042857092
##  [96,]  0.2178701  0.054999511  0.171762555
##  [97,]  0.3972811  0.219017768  0.068039368
##  [98,]  0.4340039  0.204543170  0.108670369
##  [99,]  0.1733533  1.312857679 -0.287633091
## [100,]  0.4564862  0.441522574  0.014817230
## [101,]  1.6763760 -1.401789225 -0.243822651
## [102,]  1.4205404  0.240735097 -0.138256195
## [103,]  1.5935050 -0.587176212  0.042301126
## [104,]  1.3288155 -0.203686362  0.181213131
## [105,]  1.6402652 -0.616713562 -0.089461922
## [106,]  1.8505646 -0.688498405  0.326718127
## [107,]  1.2250935  0.831667001 -0.224960376
## [108,]  1.5858751 -0.305008555  0.465630132
## [109,]  1.7859730  0.599485265  0.212110578
## [110,]  1.4253148 -2.040354443 -0.165418236
## [111,]  1.0243836 -0.843427884 -0.166432551
## [112,]  1.4939861  0.211785899 -0.056994194
## [113,]  1.4466138 -0.529277816 -0.120222875
## [114,]  1.6591566  0.627258159 -0.295201519
## [115,]  1.7420276 -0.187354854 -0.581325296
## [116,]  1.3482783 -1.004412928 -0.358566695
## [117,]  1.1961647 -0.397241969  0.153173269
## [118,]  1.2033466 -2.411226602  0.376946186
## [119,]  2.5114110  0.012174726  0.215982479
## [120,]  1.5295254  1.471408523  0.122685306
## [121,]  1.4951695 -1.062311324 -0.196042694
## [122,]  1.3346499  0.017642139 -0.298059105
## [123,]  1.9956603 -0.242900642  0.433298899
## [124,]  1.2636118  0.313696243 -0.128386147
## [125,]  1.2322754 -1.182317633 -0.001187460
## [126,]  1.1879227 -0.885675376  0.381510547
## [127,]  1.1309610  0.120140636 -0.156426009
## [128,]  0.9758279 -0.310394375 -0.090612732
## [129,]  1.6751925 -0.127692002 -0.104774151
## [130,]  1.1393670 -0.352641868  0.457330366
## [131,]  1.6918405 -0.112041099  0.280644946
## [132,]  0.9262121 -2.279778908  0.437317281
## [133,]  1.7586756 -0.171703951 -0.195906199
## [134,]  0.9906803  0.208752686  0.238863136
## [135,]  1.2826673  0.596452053  0.507967908
## [136,]  1.8339167 -0.704149308 -0.058700970
## [137,]  1.3500738 -1.507909087 -0.302623466
## [138,]  1.1002367 -0.605272175  0.165764407
## [139,]  0.9391051 -0.295919776 -0.131243732
## [140,]  1.3139630 -0.722833423 -0.148262737
## [141,]  1.6378577 -0.883818468 -0.340396881
## [142,]  1.3707607 -0.767433524 -0.452419834
## [143,]  1.4205404  0.240735097 -0.138256195
## [144,]  1.5686151 -1.091260522 -0.114780694
## [145,]  1.5662076 -1.358365428 -0.365715652
## [146,]  1.5034114 -0.573877917 -0.424379972
## [147,]  1.5756736  0.671270108 -0.204069471
## [148,]  1.2529623 -0.441842070 -0.150983828
## [149,]  1.1931451 -1.434947940 -0.292753418
## [150,]  1.0492735 -0.339343573 -0.009350732

Task 3b

Run a linear regression by using lm() command to carryout the principal component regression (PCR, not PCA!). Use just the first 2 principal components as covariates in the linear regression model. As explained before, the response variable should be Sepal length.

Solution to task 3b

Click for solution

Z = iris.pca$x[,1:2] # select the first two PCs
iris.lm <- lm(iris$Sepal.Length~Z)
iris.lm

## 
## Call:
## lm(formula = iris$Sepal.Length ~ Z)
## 
## Coefficients:
## (Intercept)         ZPC1         ZPC2  
##      5.8433       0.4230      -0.4348

Now we transform this coefficient vector to the scale of the original covariates as follows. This gives the final PCR estimator whose dimension is equal to the total number of original covariates.

iris.pca$rotation[,1:2]%*%matrix(coef(iris.lm)[-1], ncol=1)

##                   [,1]
## Sepal.Width  0.2173767
## Petal.Length 0.3853085
## Petal.Width  0.4150270

Task 3c

In practice, we do not need to do PCR ourselves in this way, as it has been implemented in the pls R package. Carryout PCR using the pcr function in R (check HERE) and compare the results.

Solution to task 3c

Click for solution

library(pls)
iris.pcr <- pcr(Sepal.Length~ Sepal.Width+Petal.Length+Petal.Width, 2, 
                scale=TRUE, data=iris) # 2 stands for number of components,
coef(iris.pcr)

## , , 2 comps
## 
##              Sepal.Length
## Sepal.Width     0.2173767
## Petal.Length    0.3853085
## Petal.Width     0.4150270